Classification Using an SVM
from typing import Tuple
import numpy as np
First we create 20 point clouds of a torus, a sphere, and a swiss roll each.
Each point cloud consists of 125 points from the surface
and 125 points of random noise.
From each point cloud we take 25 subsamples of 30 points each
and save all of these sumbsamples in the NumPy array point_clouds.
See
here for the source code.
from create_point_clouds import create_point_clouds
point_clouds = create_point_clouds(
seed = 2_000,
nb_point_clouds = 20,
nb_coarsened = 25
)
Then we plot one of these newly created point clouds (subsamples to be precise) for each surface.
from tadasets import plot3d
sphere, torus, swiss_roll = point_clouds[:,0,0]
plot3d( sphere );
plot3d( torus );
plot3d( swiss_roll );
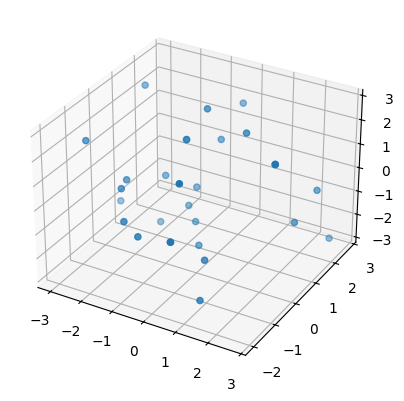
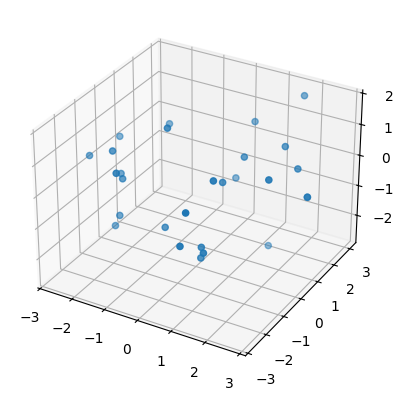
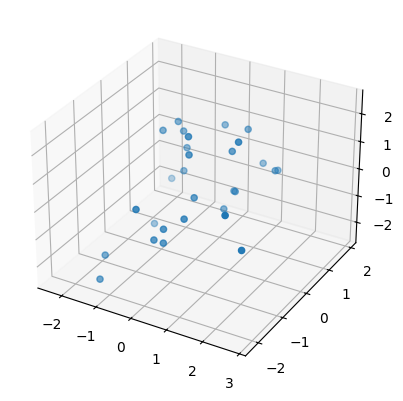
Then we compute persistence intervals for each point cloud (subsamples to be precise).
from gudhi_util import (
point_clouds_to_simplex_trees,
simplex_trees_to_persistence_intervals_in_dim
)
simplex_trees = point_clouds_to_simplex_trees( point_clouds )
persistence_intervals = [
simplex_trees_to_persistence_intervals_in_dim(
simplex_trees = simplex_trees,
dim = d
) for
d in range(3)
]
Then we merge all subsamples (persistence intervals thereof) coming from the same point cloud and we split the result into two chunks of 10 point clouds (persistence intervals thereof) from each surface each, for training and testing respectively.
import torch
nb_coarsened = persistence_intervals[0].shape[2]
def preprocess_n_split(array: np.ndarray
) -> Tuple[torch.Tensor, torch.Tensor]:
return torch.from_numpy( np.float32(np.arctan(array)) ).flatten(
start_dim = 2,
end_dim = 3
).chunk( 2, dim = 1 )
training_dgms, testing_dgms = zip(
*map( preprocess_n_split, persistence_intervals )
)
Then we create matching labels for training and testing.
labels = torch.Tensor( [[0], [1], [2]] ).long()
training_labels = labels.expand(
*training_dgms[0].shape[:2]
).flatten(0, 1).numpy()
testing_labels = labels.expand(
*testing_dgms[0].shape[:2]
).flatten(0, 1).numpy()
training_dgms_flat = [ dgm.flatten(0, 1) for dgm in training_dgms ]
testing_dgms_flat = [ dgm.flatten(0, 1) for dgm in testing_dgms ]
Then we compute the Gram matrix with respect to the inner product of Hilbert functions of the associated unravelled relative homology lattices for the training data.
from persunraveltorch.nn import HilbertGram
hilbert_gram = HilbertGram()
# Here we could set
# training_gram = hilbert_gram(training_dgms_flat, training_dgms_flat)
# However, as this would allocate a large amount of RAM at once,
# we compute the Gram matrix one row at a time instead.
training_gram = torch.cat(
[ hilbert_gram(dgm, training_dgms_flat) for
dgm in
zip(*training_dgms_flat)
]
).numpy() / nb_coarsened**2
Then we instantiate a support vector classifier and train it with the previously computed Gram matrix.
from sklearn import svm, metrics
clf = svm.SVC( kernel = 'precomputed' )
clf.fit( training_gram, training_labels )
SVC(kernel='precomputed')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
| C | 1.0 | |
| kernel | 'precomputed' | |
| degree | 3 | |
| gamma | 'scale' | |
| coef0 | 0.0 | |
| shrinking | True | |
| probability | False | |
| tol | 0.001 | |
| cache_size | 200 | |
| class_weight | None | |
| verbose | False | |
| max_iter | -1 | |
| decision_function_shape | 'ovr' | |
| break_ties | False | |
| random_state | None |
Then we compute the Gram matrix for testing and we test the previously trained support vector classifier.
from gram_test import GramTest
support_indices = torch.from_numpy( np.int64(clf.support_) )
gram_test = GramTest(
gram = hilbert_gram,
support_indices = support_indices,
len_train = len( training_dgms_flat[0] ),
support_vectors = [
intervals[support_indices] for
intervals in
training_dgms_flat
]
)
testing_gram = torch.cat(
[ gram_test(dgm) for dgm in zip(*testing_dgms_flat) ]
).numpy() / nb_coarsened**2
print(f"Model accuracy: {100 * metrics.accuracy_score(testing_labels, clf.predict(testing_gram)):>0.1f}%\n")
Model accuracy: 96.7%